[자료구조] 그래프를 코드로 나타내는 방법 (feat. C++)

그래프란?

https://sanhan.tistory.com/entry/자료구조-그래프와-트리

1. 인접 행렬 (Adjacency Matrix) 로 표현

행렬에 간선 정보를 담는 방식.

각 행이 간선의 시작 노드를 나타낸다. (0번째 행은 0번 노드에서 시작해서 다른 노드로 향하는 간선들의 정보이다.)

행렬값: 연결되었으면 1 (가중치가 있다면 가중치를 저장), 그렇지 않으면 0

방향 그래프

코드 - 2차원 배열

#include <iostream>

using namespace std;

void addEdge(int** matrix, int from, int to){
	matrix[from][to] = 1;
}

int main()
{
	int vn = 4; // 정점(Node, Vertex)의 개수
	int **graph = new int *[vn];
	for (int i = 0; i < vn; i++)
	{
		graph[i] = new int[vn];
		memset(graph[i], 0, sizeof(int) * vn);    
	}			//메모리 0으로 초기화
	
	addEdge(graph, 0, 1);	// from 0 to 1
	addEdge(graph, 0, 2);	// from 0 to 2
	addEdge(graph, 0, 3);	// from 0 to 3
	addEdge(graph, 1, 2);	// from 1 to 2
	addEdge(graph, 3, 2);	// form 3 to 2
	
	for (int i = 0; i < vn; ++i)
	{
		for (int j = 0; j < vn; ++j)
			cout << graph[i][j] << " ";
		cout << "\n";
	}
	
	for (int i = 0; i < vn; ++i)
	{
		delete[] graph[i];
	}
	delete[] graph;
}

/*
0 1 1 1 
0 0 1 0 
0 0 0 0 
0 0 1 0 
*/

무방향 그래프

무향방 그래프는 양방향 그래프와 같다.

점선으로 표시된 대각선을 기준으로 대칭을 이룸.

코드 - 2차원 배열

#include <iostream>

using namespace std;

void addEdge(int** matrix, int v1, int v2){
	matrix[v1][v2] = 1;
	matrix[v2][v1] = 1;
}

int main()
{
	int vn = 4; // 정점의 개수
	int **graph = new int *[vn];
	for (int i = 0; i < vn; i++)
	{
		graph[i] = new int[vn];
		memset(graph[i], 0, sizeof(int) * vn);
	}			//메모리 0으로 초기화

	addEdge(graph, 0, 1);
	addEdge(graph, 0, 2);
	addEdge(graph, 0, 3);
	addEdge(graph, 1, 2);
	addEdge(graph, 2, 3);

	for (int i = 0; i < vn; ++i)
	{
		for (int j = 0; j < vn; ++j)
			cout << graph[i][j] << " ";
		cout << "\n";
	}

	for (int i = 0; i < vn; ++i)
	{
		delete[] graph[i];
	}
	delete[] graph;
}

/*
0 1 1 1 
1 0 1 0 
1 1 0 1 
1 0 1 0 
*/

2. 인접 리스트 (Adjacency List) 로 표현

각 행이 시작 노드가 된다.

각 행마다 해당 노드에 연결된 간선의 도착 노드를 저장한다.

방향 그래프

코드 - vector 사용

#include <iostream>
#include <vector>

using namespace std;

void addEdge(vector<int>* list, int v1, int v2){
	list[v1].push_back(v2);
}

int main()
{
	int vn = 4; 			// 정점의 개수
	vector<int> graph[vn];
	addEdge(graph,0, 1);
	addEdge(graph,0, 2);
	addEdge(graph,0, 3);
	addEdge(graph,1, 2);
	addEdge(graph,3, 2);

	for (int i = 0; i < vn; ++i)
	{
		cout << i << " -> ";
		vector<int>::iterator itor = graph[i].begin();
		vector<int>::iterator end = graph[i].end();
		for (; itor != end; itor++)
			cout << *itor << " ";
		cout << "\n";
	}
	 return 0;
}

/*
0 -> 1 2 3 
1 -> 2 
2 -> 
3 -> 2 
*/

무방향 그래프

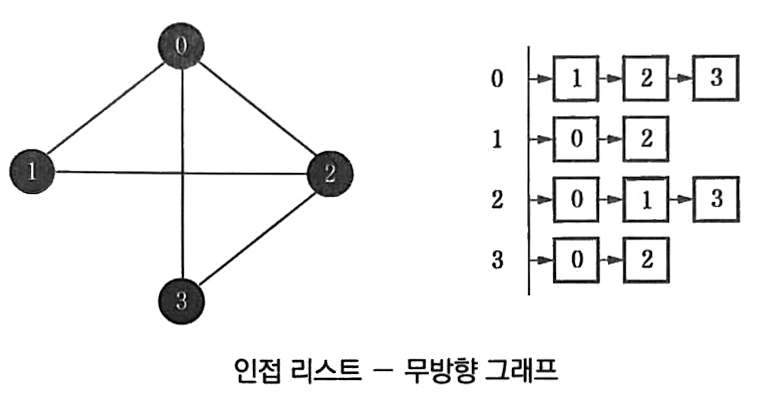
무방향은 역시 양방향으로 생각해서 적용한다.

코드 - vector 사용

#include <iostream>
#include <vector>

using namespace std;

void addEdge(vector<int>* list, int v1, int v2){
	list[v1].push_back(v2);
	list[v2].push_back(v1);
}

int main()
{
	int vn = 4; 			// 정점의 개수
	vector<int> graph[vn];
	addEdge(graph,0, 1);
	addEdge(graph,0, 2);
	addEdge(graph,0, 3);
	addEdge(graph,1, 2);
	addEdge(graph,2, 3);

	for (int i = 0; i < vn; ++i)
	{
		cout << i << " -> ";
		vector<int>::iterator itor = graph[i].begin();
		vector<int>::iterator end = graph[i].end();
		for (; itor != end; itor++)
			cout << *itor << " ";
		cout << "\n";
	}
	 return 0;
}
/*
0 -> 1 2 3 
1 -> 0 2 
2 -> 0 1 3 
3 -> 0 2 
*/

각 표현 방식의 장단점 (인접 행렬 vs 인접 리스트)

	인접 행렬	인접 리스트
장점	특정 노드로 가는 간선이  있는지 여부를 O(1)만에 알아 낼 수 있다 예를 들어, 0에서 3으로 가는 간선이 있는지 알기 위해선 배열[0][3]의 값을 보면 알수 있기 떄문.	간선의 개수가 적을 수록 메모리를 덜 차지한다.
단점	간선의 개수와 상관없이 항상 N제곱의 메모리를 사용한다.	특정 노드로 가는 간선이 있는지 알기 위해선 순차 탐색을 하며 살펴봐야 한다. O(N) 0에서 3으로 가는 간선이 있는지 알기 위해선 0행에 있는 데이터를 순차 탐색하며 '3'이 있는지를 살펴봐야 한다.

 

 

TRANSLATE with x

English

Arabic	Hebrew	Polish
Bulgarian	Hindi	Portuguese
Catalan	Hmong Daw	Romanian
Chinese Simplified	Hungarian	Russian
Chinese Traditional	Indonesian	Slovak
Czech	Italian	Slovenian
Danish	Japanese	Spanish
Dutch	Klingon	Swedish
English	Korean	Thai
Estonian	Latvian	Turkish
Finnish	Lithuanian	Ukrainian
French	Malay	Urdu
German	Maltese	Vietnamese
Greek	Norwegian	Welsh
Haitian Creole	Persian

 

TRANSLATE with

COPY THE URL BELOW

Back

EMBED THE SNIPPET BELOW IN YOUR SITE

Enable collaborative features and customize widget: Bing Webmaster Portal

Back